pysimenv 패키지를 이용한 동역학 시뮬레이션 예제 (1)
선형 시스템의 스텝 반응 시뮬레이션하기
개요
pysimenv는 제가 동역학 시뮬레이션을 쉽게 할 수 있도록 하기 위해 작성한 파이썬 패키지입니다. pysimenv 패키지를 작성하면서 다음과 같은 점들을 염두에 두고 작성했습니다.
- 새로운 동역학 시스템과 제어기, 시뮬레이션 모델을 정의하는 코드를 작성하기 쉽도록 하기
- 이미 작성 또는 개발된 코드의 활용성을 높이기
- 시뮬레이션을 쉽게 수행할 수 있도록 하기
- 시뮬레이션 시간을 단축하기
- 시뮬레이션 데이터를 활용하기 쉽도록 하기
제어 및 유도 연구를 하는 많은 사람들이 유용하게 쓰면 좋겠다는 바람에 패키지 쓰는 법에 대해서 포스트를 몇 개 연재해볼까 합니다. 패키지 코드와 (영어로 작성된) 예제 등은 아래 링크에서 확인해볼 수 있습니다.
첫 번째 포스트에서는 패키지를 이용해서 선형 시스템을 정의하고, 스텝 반응을 시뮬레이션하는 예제에 대해 살펴보겠습니다.
동역학 시스템 정의
다음과 같은 형태의 전달함수를 가지는 이차 선형 시스템을 고려하겠습니다. \[G(s) = \frac{\omega_{n}^{2}}{s^{2} + 2\zeta\omega_{n} + \omega_{n}^{2}}\]
여기에서 \(\omega_{n}\)은 natural frequency, \(\zeta\)는 damping ratio를 나타냅니다. 시뮬레이션을 하려면 시스템을 상태공간 방정식의 형태로 나타내야 하는데, 시스템의 상태를 \(x=[x_{1}\,x_{2}]^{T}\), 제어입력을 \(u\)라 한 뒤 다음과 같은 상태공간 방정식으로 나타낼 수 있습니다. \[\dot{x} = \begin{bmatrix} 0 & 1 \\ -\omega_{n}^{2} & -2\zeta\omega_{n} \end{bmatrix}x + \begin{bmatrix} 0 \\ \omega_{n}^{2} \end{bmatrix}u\]
이것을 코드를 이용하여 구현해보겠습니다.
먼저, 시뮬레이션에 필요한 모듈을 불러옵니다.
import numpy as np
import matplotlib.pyplot as plt
from pysimenv.core.base import DynSystem
from pysimenv.core.simulator import Simulator
main 함수를 정의해주고
def main():
그 안에 deriv_fun이라는 이름으로 동역학 방정식을 나타내는 함수를 정의합니다. natural frequency의 값은 1, damping ratio의 값은 0.8로 정했습니다.
def main():
def deriv_fun(x, u):
omega = 1.
zeta = 0.8
A = np.array([[0, 1.], [-omega**2, -2*zeta*omega]])
B = np.array([[0.], [omega**2]])
x_dot = A.dot(x) + B.dot(u)
return {'x': x_dot}
동역학 방정식을 나타내는 함수는 시스템의 상태를 나타내는 Numpy 배열들과 제어입력을 나타내는 Numpy 배열들을 입력으로 받아, 각 상태변수에 대응되는 미분 값을 반환해주는 역할을 합니다. 이 때, 함수의 반환 값은 상태변수의 이름과 미분 값을 각각 key, value로 하는 dictionary 자료형으로 정의해야 합니다. 위에서는 상태변수의 이름이 x이기 때문에 x를 key로 하고 x_dot을 value로 하여 반환 값을 정의했습니다.
deriv_fun 함수를 이용하여 동역학 시스템을 정의합니다.
sys = DynSystem(
initial_states={'x': np.zeros(2)},
deriv_fun=deriv_fun
)
시스템의 초기 상태는 initial_states 인자를 이용해서 정의할 수 있으며, 시스템의 동역학 방정식은 deriv_fun 인자를 이용해서 정의할 수 있습니다. 더 복잡한 동역학 방정식을 정의하기 위해 클래스 overriding 등을 이용할 수 있는데, 그 방법에 대해서는 후속 포스트에서 살펴보겠습니다. 초기 상태 값을 지정할 때에는 상태변수의 이름과 대응되는 초기 값을 각각 key, value로 하는 dictionary 자료형을 이용해야 합니다.
시뮬레이션 수행 및 결과 시각화
동역학 모델을 정의했으니, 이를 시뮬레이션하기 위한 시뮬레이터를 정의하고 적분 간격을 0.01초로 하여 10초 동안 시뮬레이션을 수행하도록 합니다. 제어입력의 값으로는 unit step input에 해당하는 1을 넘겨줍니다.
simulator = Simulator(sys)
simulator.propagate(dt=0.01, time=10., save_history=True, u=np.array([1.]))
시뮬레이션 데이터는 다음과 같이 얻을 수 있습니다.
t = sys.history('t')
x = sys.history('x')
u = sys.history('u')
sys.history(key)는 각각 (시간 축, 변수의 차원 축)으로 이루어진 Numpy 배열을 반환해주는 메소드입니다. 예를 들어, 이 예제에서는 0.01초 간격으로 10초 동안 시뮬레이션을 수행했으므로 데이터는 1,001개가 생성되고, t와 x, u는 각각 크기가 (1001, ), (1001, 2), (1001, 1)인 Numpy 배열로 반환됩니다.
마지막으로, 시뮬레이션 데이터를 시각화하는 코드를 추가하겠습니다.
fig, ax = plt.subplots()
for i in range(2):
ax.plot(t, x[:, i], label="x_" + str(i + 1))
ax.set_xlabel("Time (s)")
ax.set_ylabel("x")
ax.grid()
ax.legend()
fig, ax = plt.subplots()
ax.plot(t, u)
ax.set_xlabel("Time (s)")
ax.set_ylabel("u")
ax.grid()
plt.show()
전체 코드는 다음과 같습니다.
import numpy as np
import matplotlib.pyplot as plt
from pysimenv.core.base import DynSystem
from pysimenv.core.simulator import Simulator
def main():
def deriv_fun(x, u):
omega = 1.
zeta = 0.8
A = np.array([[0, 1.], [-omega**2, -2*zeta*omega]])
B = np.array([[0.], [omega**2]])
x_dot = A.dot(x) + B.dot(u)
return {'x': x_dot}
sys = DynSystem(
initial_states={'x': np.zeros(2)},
deriv_fun=deriv_fun
)
simulator = Simulator(sys)
simulator.propagate(dt=0.01, time=10., save_history=True, u=np.array([1.]))
t = sys.history('t')
x = sys.history('x')
u = sys.history('u')
fig, ax = plt.subplots()
for i in range(2):
ax.plot(t, x[:, i], label="x_" + str(i + 1))
ax.set_xlabel("Time (s)")
ax.set_ylabel("x")
ax.grid()
ax.legend()
fig, ax = plt.subplots()
ax.plot(t, u)
ax.set_xlabel("Time (s)")
ax.set_ylabel("u")
ax.grid()
plt.show()
if __name__ == "__main__":
main()
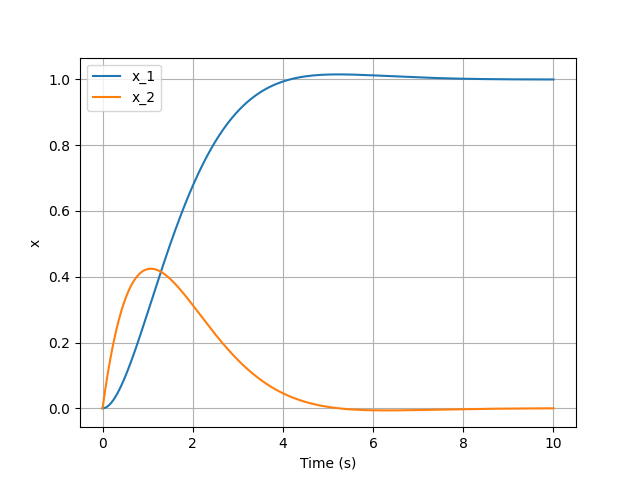
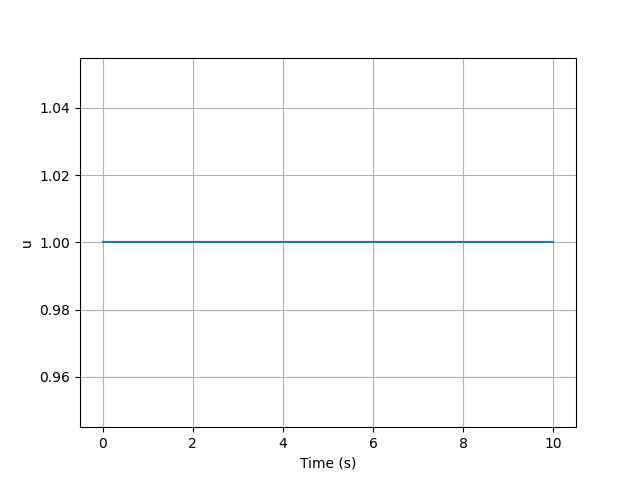
코드를 실행하면 시뮬레이션 결과를 얻을 수 있습니다.
위쪽 그림이 상태변수에 대한 그래프, 아래쪽 그림이 제어입력에 대한 그래프입니다.